
CATEGORÍAS
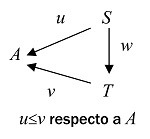
 | MENTAL vs. TEORÍA DE CATEGORÍAS |
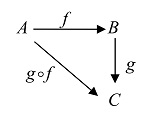
|
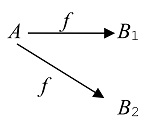
|
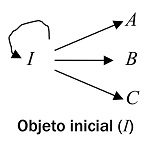
|
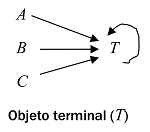
|
|
|
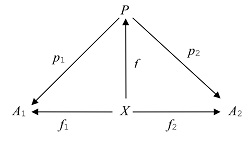
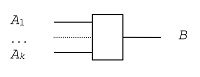
| X→A1×A2 |
| X→A1, X→A2 |
|
| f= | { | f1 |
| f2 |
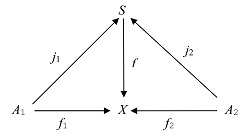
| A1+A2→X |
| A1→X, A2→X |
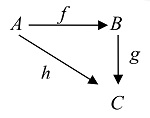
| X→YZ |
| Z×X→Y |
|
|
| Propiedad | Colímites | Límites |
| Objeto especial | Objeto inicial: 0 | Objeto terminal: 1 |
| Operación | Suma de objetos | Producto de objetos |
| Operación nula | 0+A = A | 1×A = A |
| Conjunto cociente C/X (para todo objeto X) | C/X tiene sumas | C/X tiene productos |
|
|
|
|
α) y la expresión nula (θ).